И так что мы имеем? Я не буду углубляться во все
разновидности рулетки, как американская или французская и не буду сильно анализировать, дабы не прослыть скучным теоретиком,приведу лишь почти итоговые выкладки, так как это тема не одной книги.
Остановлюсь на самой
простой модели - это европейская рулетка. Рулетка, в которой 37 ячеек, из них
числа от 1 до 36 и 0-зеро. Причем исход выпадения каждой равновероятен.
В итоге мы имеем конечное вероятностное пространство 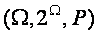 , где
, где
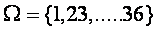 ,
, 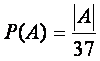 , для любого
, для любого 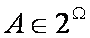 .
.
Назовем ставкой S тройку 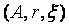 , где A-
некоторое событие,
, где A-
некоторое событие, 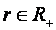 , где
, где 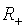 это множество целых
неотрицательных чисел. А
это множество целых
неотрицательных чисел. А 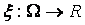 - случайная величина.
- случайная величина.
Событие A соответствует выигрышному событию, r- размеру ставки в любых единицах
(рублях, евро и т. д),
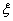 -правилу ставки, а математическое ожидание
-правилу ставки, а математическое ожидание 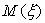 -прибыльности ставки. Для ставок на один номер имеем:
-прибыльности ставки. Для ставок на один номер имеем: 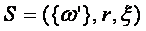 , где
, где 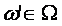 и
и 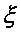 определяется функцией
определяется функцией 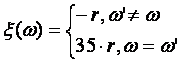
И прибыльность самой ставки равна:
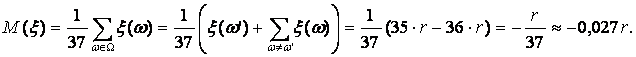
Аналогично, если опустить подробности и взять ставки на
шансы, например: черное-красное, то получим:  , а прибыльность равна:
, а прибыльность равна:
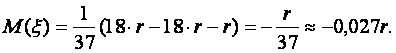
Аналогично рассуждая можно определить, что прибыльность вобщем случае
равна 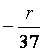 .
.
Вроде бы мы постоянно находимся в убытке, судя по выводам.
Так оно и есть, только в том случае если рассматривать бесконечный промежуток времени. Но есть и
другая величина, характеризующая выигрыш-это Ваше первоначальное преимущество
перед казино или дисперсия случайной величины выпадения определенного номера.
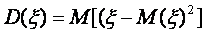 и в силу линейности
математического ожидания можно получить формулу
и в силу линейности
математического ожидания можно получить формулу
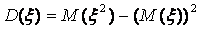 -выражение может иметь положительную величину при
определенном виде ставок и иметь весьма внушительное значение. Чем больше сумма
Вашего депозита или чем меньше размер ставки - тем больше Ваше преимущество.
Особенно на начальном этапе, и этим можно воспользоваться для получения
прибыли.
-выражение может иметь положительную величину при
определенном виде ставок и иметь весьма внушительное значение. Чем больше сумма
Вашего депозита или чем меньше размер ставки - тем больше Ваше преимущество.
Особенно на начальном этапе, и этим можно воспользоваться для получения
прибыли.
